When teaching journalism students about AI, it is essential to present complex mathematical ideas in an accessible manner. Simplifying these concepts allows students to grasp both the fostering of digital literacy and the critical understanding of technology. Central to this understanding are neural networks, which underpin many AI applications, including large language models.
A neural network works like a very advanced calculator, or more simply, a machine that finds patterns in data. One layer spots basic shapes, the next puts them together, and the final layer combines and makes a decision.
A network learns by being trained on a set of labeled examples. These examples help it correct its mistakes. The network picks up patterns from the data it receives. If the data has biases, the network will reproduce them. In general, how the network acts depends entirely on its training data. If the data is incomplete, biased, or mislabeled, the network will make mistakes for those reasons.
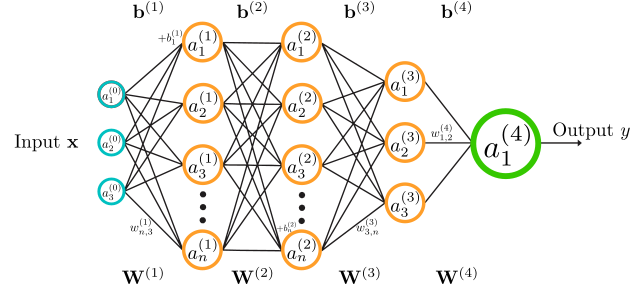
A neural network consists of an input layer, an output layer, and at least one hidden layer in between. Each layer has several neurons. In the hidden layers, each neuron has its own bias, so a layer with X neurons has X biases. For example, in image classification:
- the first layer looks at and observes raw details like edges and shades,
- the next layer combines this information to find shapes and textures,
- the final layers decide what the image shows, such as whether it is a cat or not.
To understand the number of parameters, observe the connections: between two layers, each neuron in the first layer is connected to all neurons in the next layer. We therefore obtain:
- X × Y weights, if the first layer contains X neurons and the second Y,
- + Y biases, one per neuron in the next layer.
These weights and biases together constitute the network’s parameters.
Having many parameters allows the network to model complex phenomena. Still, it also requires a lot of data to avoid overfitting, a phenomenon in which the model learns so well from its training data that it can no longer generalize to new examples.
The network starts by making a calculation and giving an output. It then compares this output to the honest answer to compute the loss, which is a measure of how wrong it was. For predicting numbers, Mean Squared Error (MSE) is often used. For tasks like determining whether an image contains a cat, cross-entropy is used because it measures both the error and the model’s confidence.
The models don’t provide an « answer, » but a probability. This is fundamental to understanding what an AI prediction is. For example, a network doesn’t say « it’s a cat » but « there’s a 92% chance it’s a cat. » The decisions are therefore probabilistic.
In the first iteration, the weights are randomly chosen; as a result, the predictions are poor, and the loss is generally high. But this loss indicates in which direction the network needs to adjust its parameters. The larger the error, the more significant the initial corrections.
To reduce this error, the system uses gradient descent, an algorithm that gradually adjusts the parameters to bring the prediction closer to the truth. This process is similar to finding the lowest point in a landscape by taking small steps downhill, always following the steepest descent. The mechanism that precisely calculates how each weight should be modified is called backpropagation, which works by tracing back the steps taken to identify precisely where and how to adjust to move closer to the correct answer. By repeating this process across many examples, the network gradually improves: it learns.
After each calculation, an activation function determines whether a neuron is highly, weakly, or not activated at all. This introduces a form of « decision-making » into the network, preventing it from behaving like a simple linear equation.
That being said, a neural network excels at the tasks for which it has been trained, but it can make complete mistakes as soon as it steps outside its domain.
What is the purpose of a neural network in journalism?
- automatically transcribe interviews,
- analyze images (e.g., fact-checking),
- recommend content,
- detect deepfakes,
- classify documents.



